Gallery

Square Lattice

The traditional Hofstadter butterfly with nearest-neighbor hoppings on the square lattice. The red-blue color scheme is chosen to mimic Fig.1(a,b) from [DiColandrea22].

butterfly -mod Hofstadter -q 499 -lat square -col plane -pal red-blue -wan -dpi 500 -save

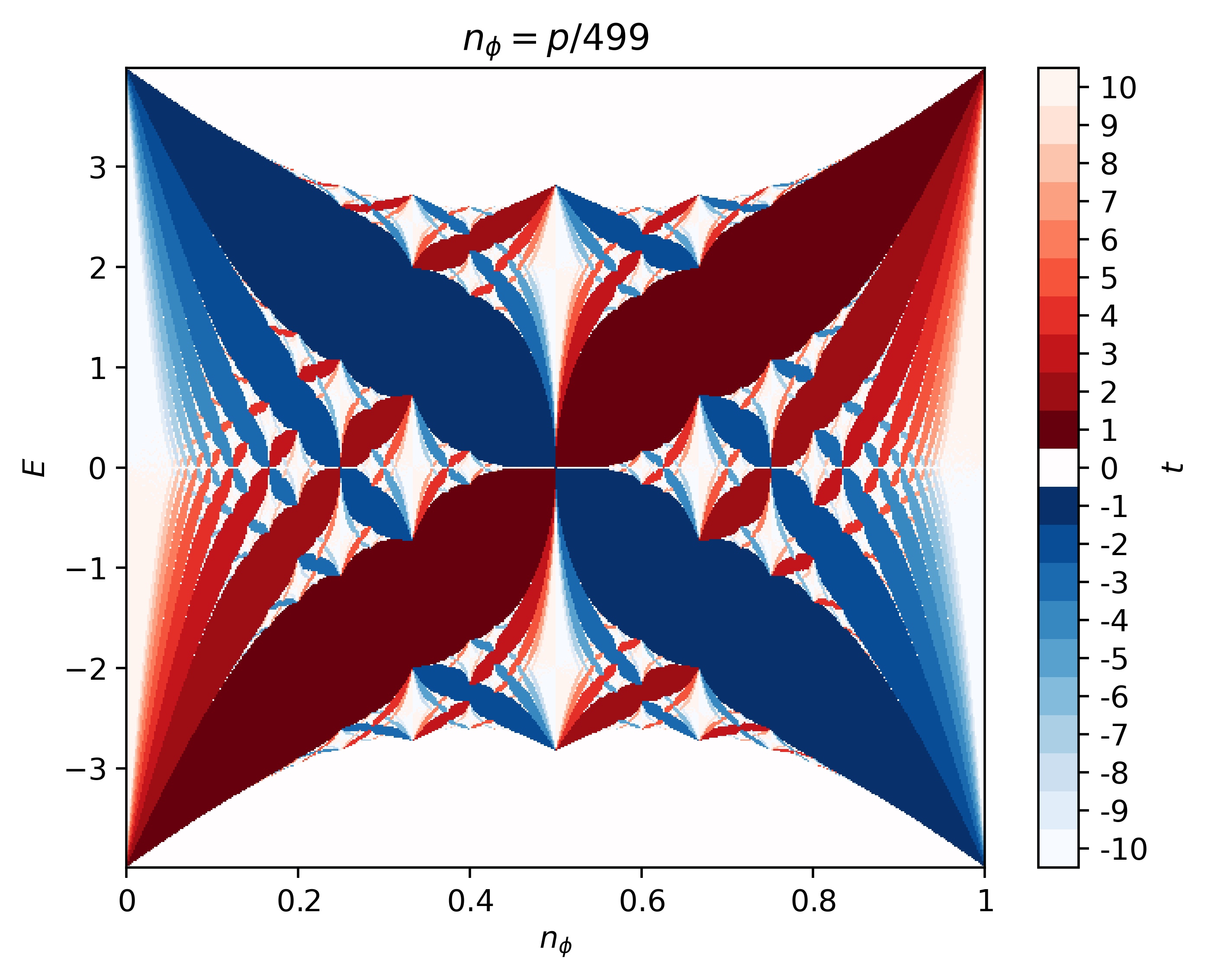
_images/butterfly_square_q_499_t_1_col_plane_red-blue_dpi_500.png

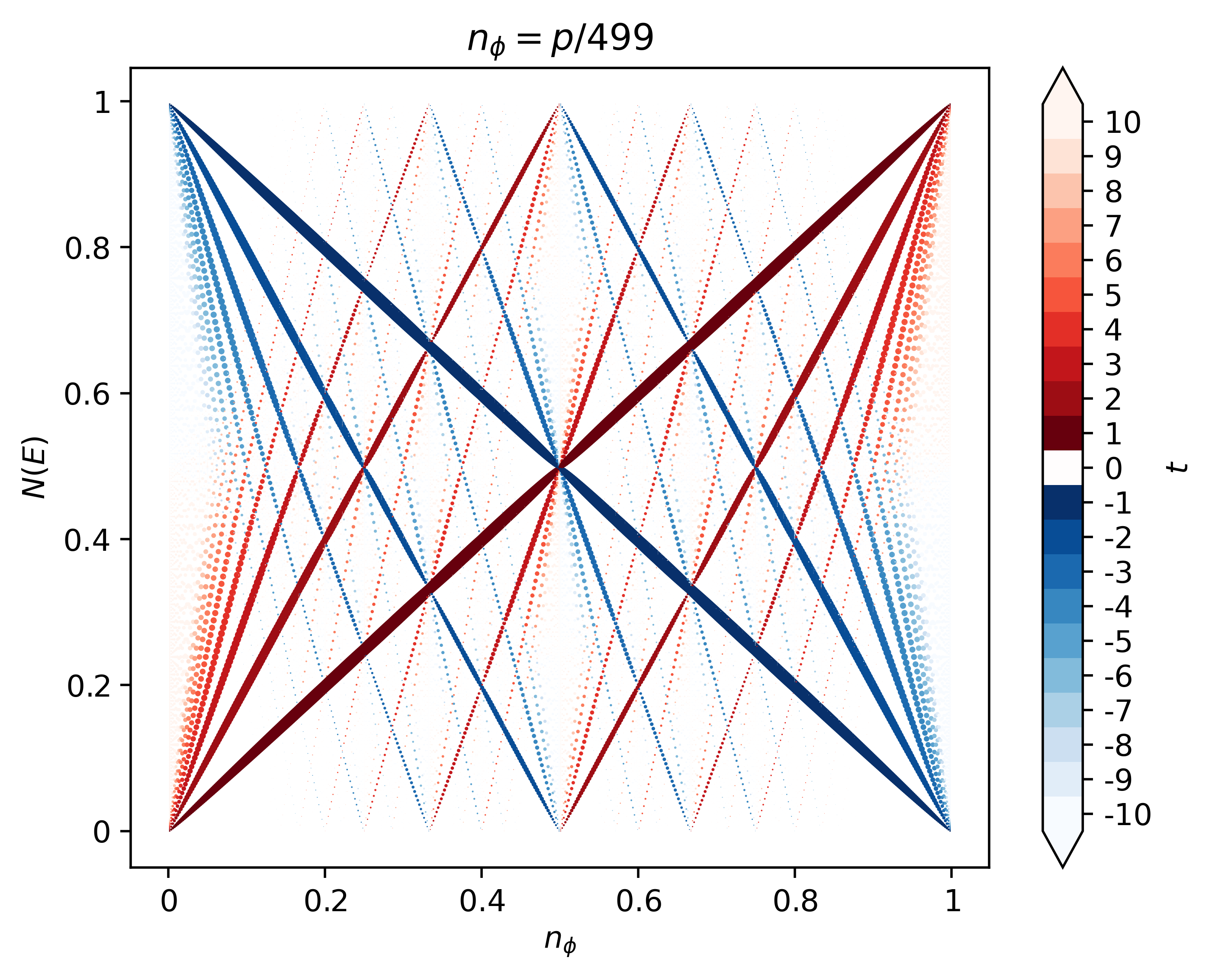
_images/wannier_square_q_499_t_1_col_plane_red-blue_dpi_500.png

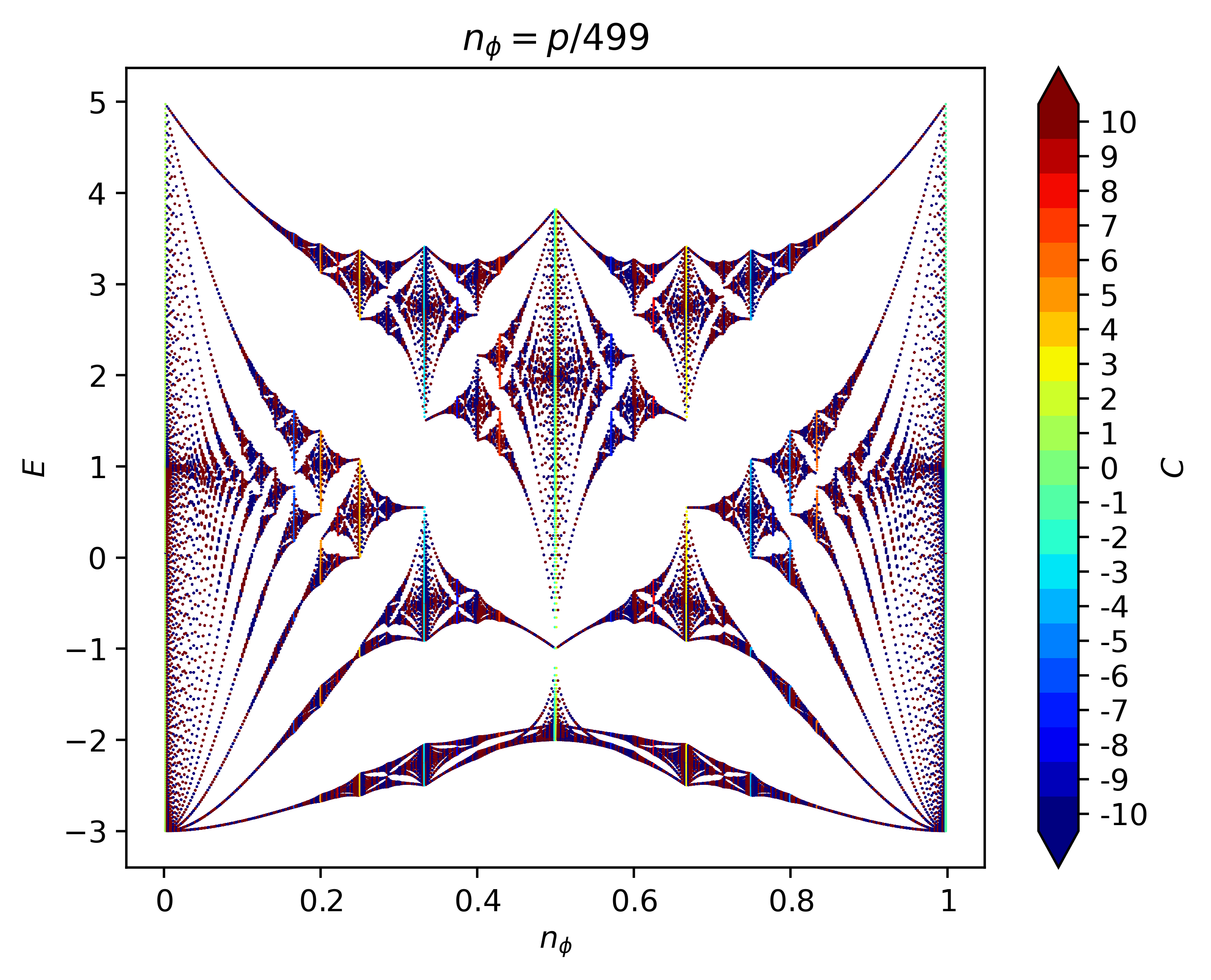
The Hofstadter model with 1st and 3rd nearest-neighbor hoppings on the square lattice, with hopping amplitudes chosen such that it is at the zero-quadratic point. The jet point color scheme is chosen to mimic Fig.2(b) from [Andrews23]. This butterfly is plotted in Fig.2 of [Bauer22].

butterfly -mod Hofstadter -q 499 -lat square -t 1 0 " -0.25" -col point -pal jet -dpi 500 -save

Note

The Hofstadter Hamiltonian is defined with an overall minus sign in HofstadterTools. Hence, -t 1 translates to an effective hopping strength of -1 for nearest-neighbor terms, and so on.

_images/butterfly_square_q_499_t_1_0_-0.25_col_point_jet_dpi_500.png

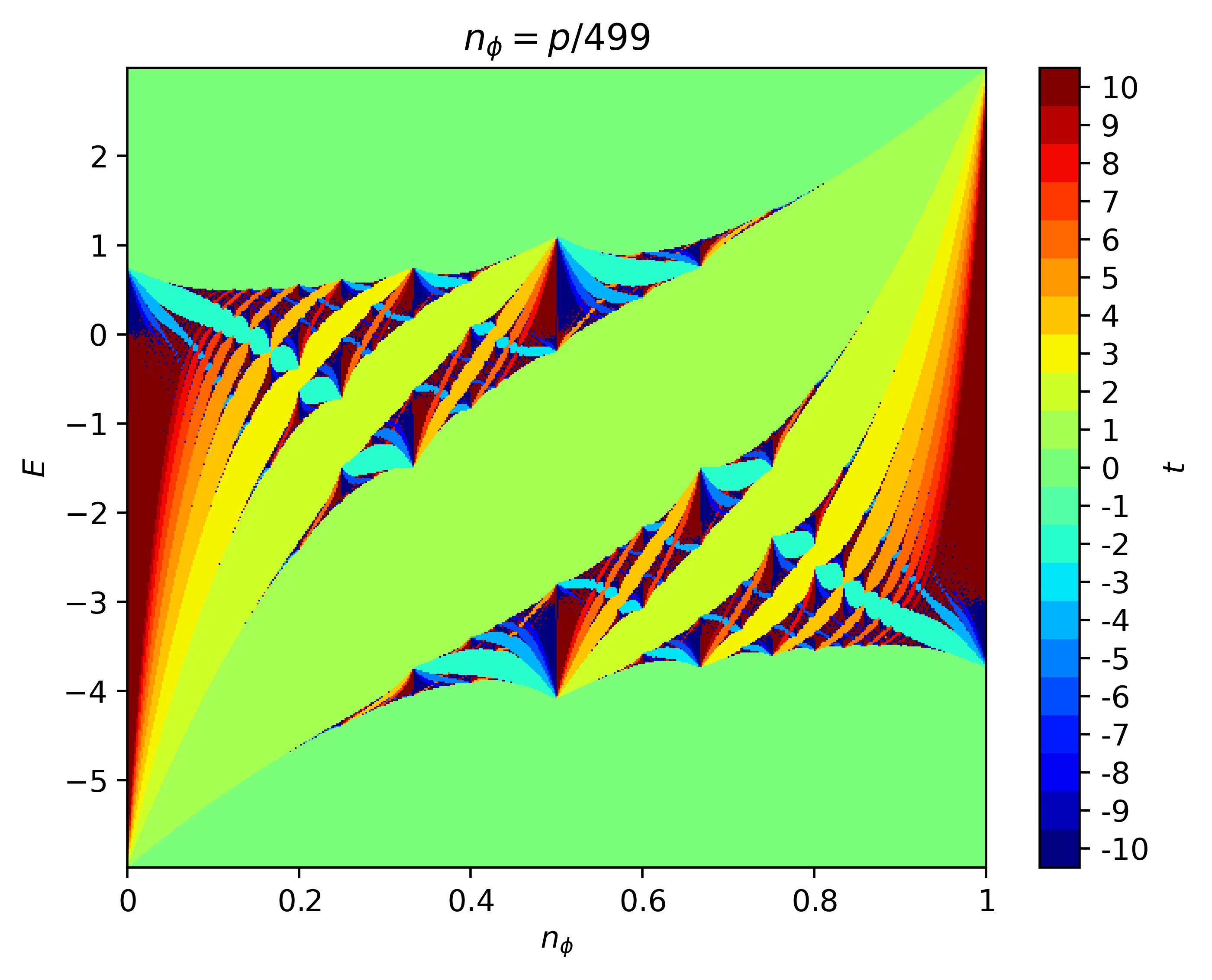
Triangular Lattice

The Hofstadter model with nearest-neighbor hoppings on the triangular lattice. Note that in this case, we keep the default definition of the flux density defined with respect to the lattice unit cell area. In several works, e.g. [Stegmaier22], the flux density is defined with respect to the minimal hopping plaquette area, which reveals the entire spectrum.

butterfly -mod Hofstadter -q 499 -lat triangular -col plane -pal jet -dpi 500 -save

_images/butterfly_triangular_q_499_t_1_col_plane_jet_dpi_500.png

Bravais Lattice

The Hofstadter model on a Bravais lattice with an obliqueness angle of 67/180 in units of \(\\\pi\), in between the square and triangular lattices. The hopping amplitudes are similar (but not identical) to those used in Fig.4(c) of [Yilmaz17].

butterfly -mod Hofstadter -q 499 -lat bravais -theta 67 180 -t 0.5 0.2 -dpi 500 -save

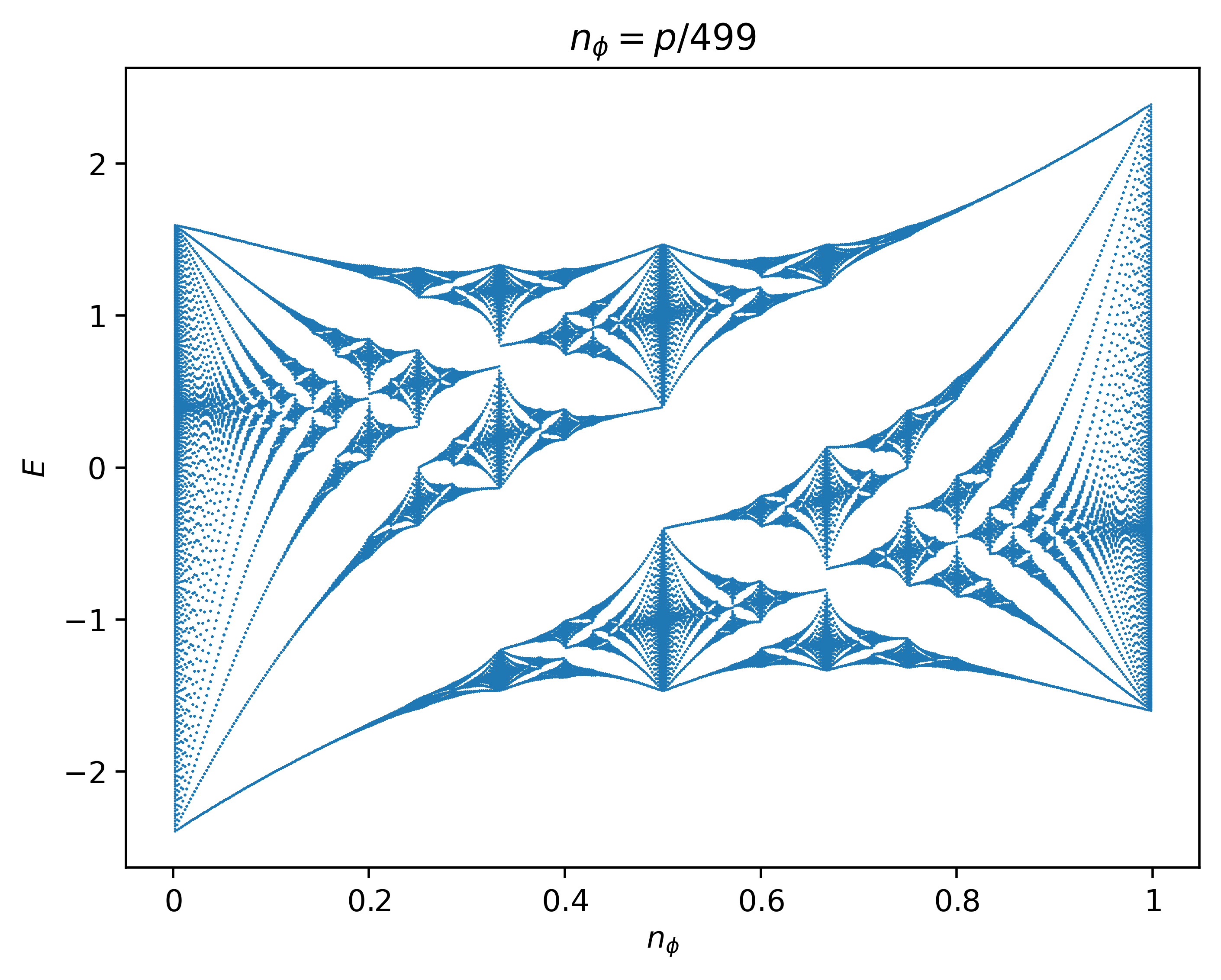
_images/butterfly_bravais_q_499_t_0.5_0.2_alpha_1_theta_67_180_dpi_500.png

Honeycomb Lattice

The Hofstadter model with nearest-neighbor hoppings on a honeycomb lattice. The color scheme is chosen to mimic the one made famous by Avron in his original paper [Avron03]. This butterfly is also plotted in Fig.5 of [Agazzi14]. For aesthetics, we increase the dpi to 1000 and plot the spectrum in art mode, which removes the axes/labels and makes the white color transparent.

butterfly -mod Hofstadter -q 499 -lat honeycomb -col plane -art -wan -dpi 1000 -save

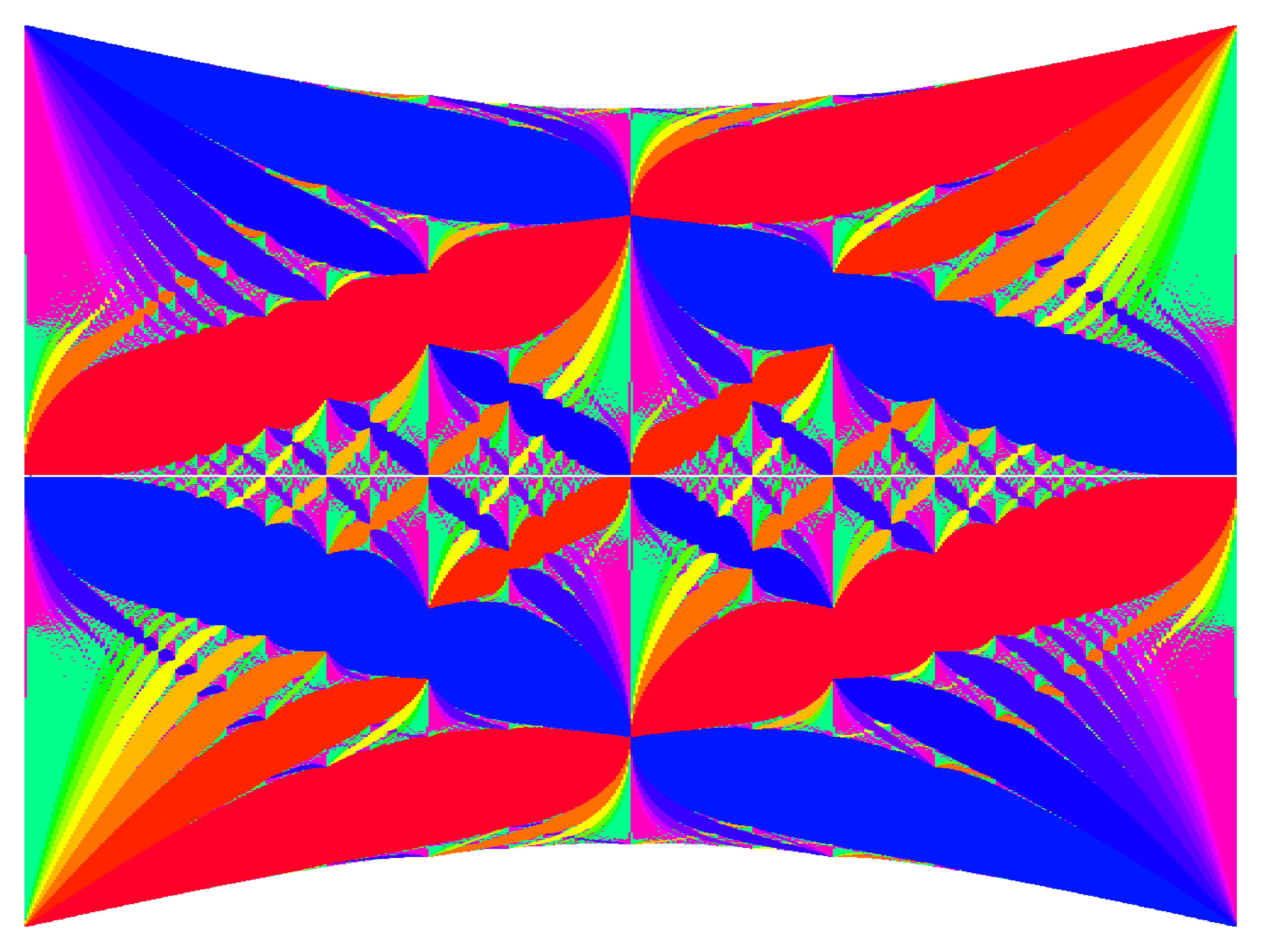
_images/butterfly_honeycomb_q_499_t_1_alpha_1_theta_1_3_col_plane_avron_art_dpi_1000.png

_images/wannier_honeycomb_q_499_t_1_alpha_1_theta_1_3_col_plane_avron_art_dpi_1000.png

The Hofstadter model with equal-amplitude 1st and 2nd nearest-neighbor hopping on the honeycomb lattice. In this case, the minimal plaquette area enclosed by particle hopping is 6 times smaller than the unit cell area, and so we append --periodicity 6 to resolve the entire butterfly spectrum and fix any aperiodicity.

butterfly -mod Hofstadter -q 499 -lat honeycomb -t 1 1 -period 6 -dpi 500 -save

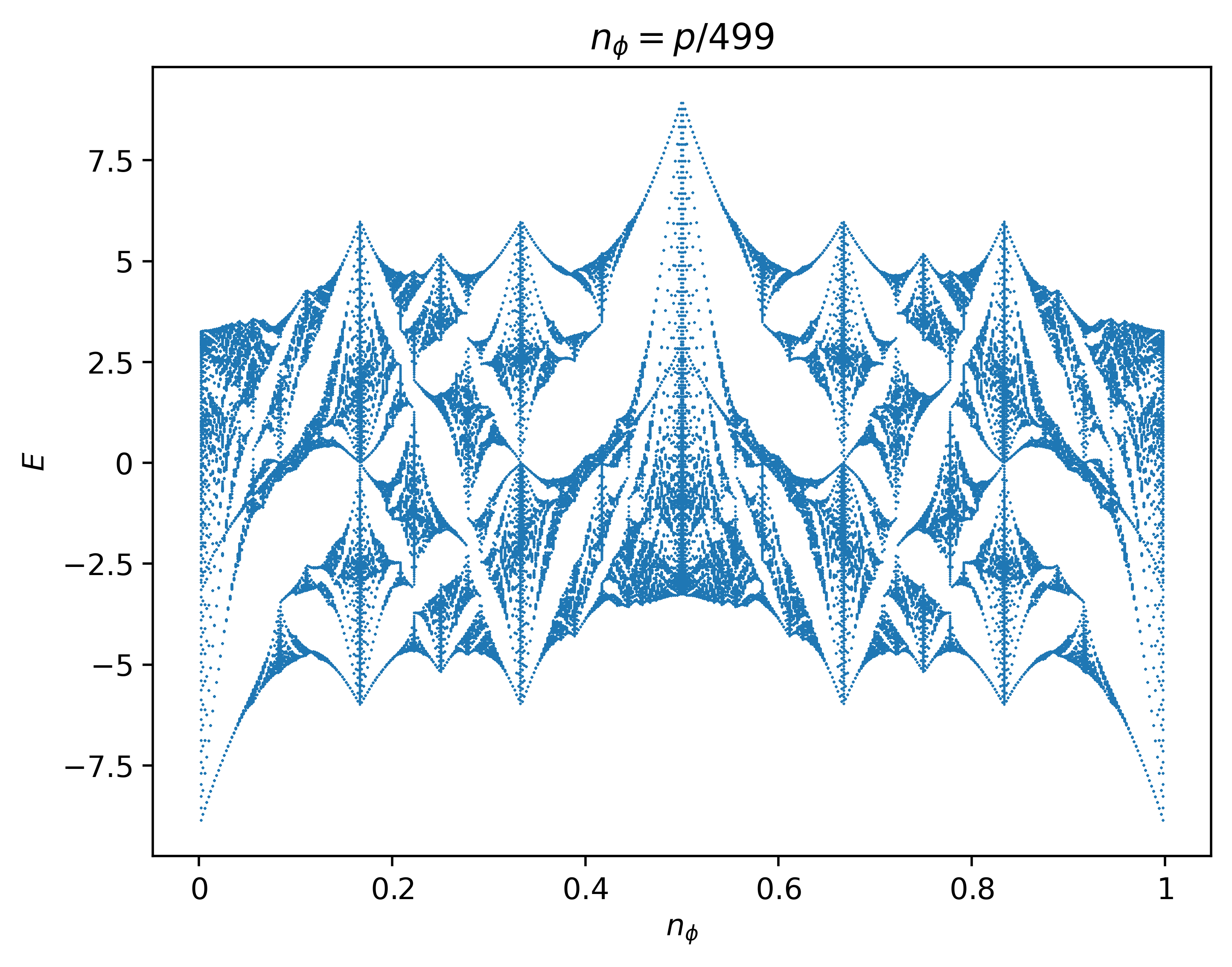
_images/butterfly_honeycomb_q_499_t_1_1_alpha_1_theta_1_3_period_6_dpi_500.png

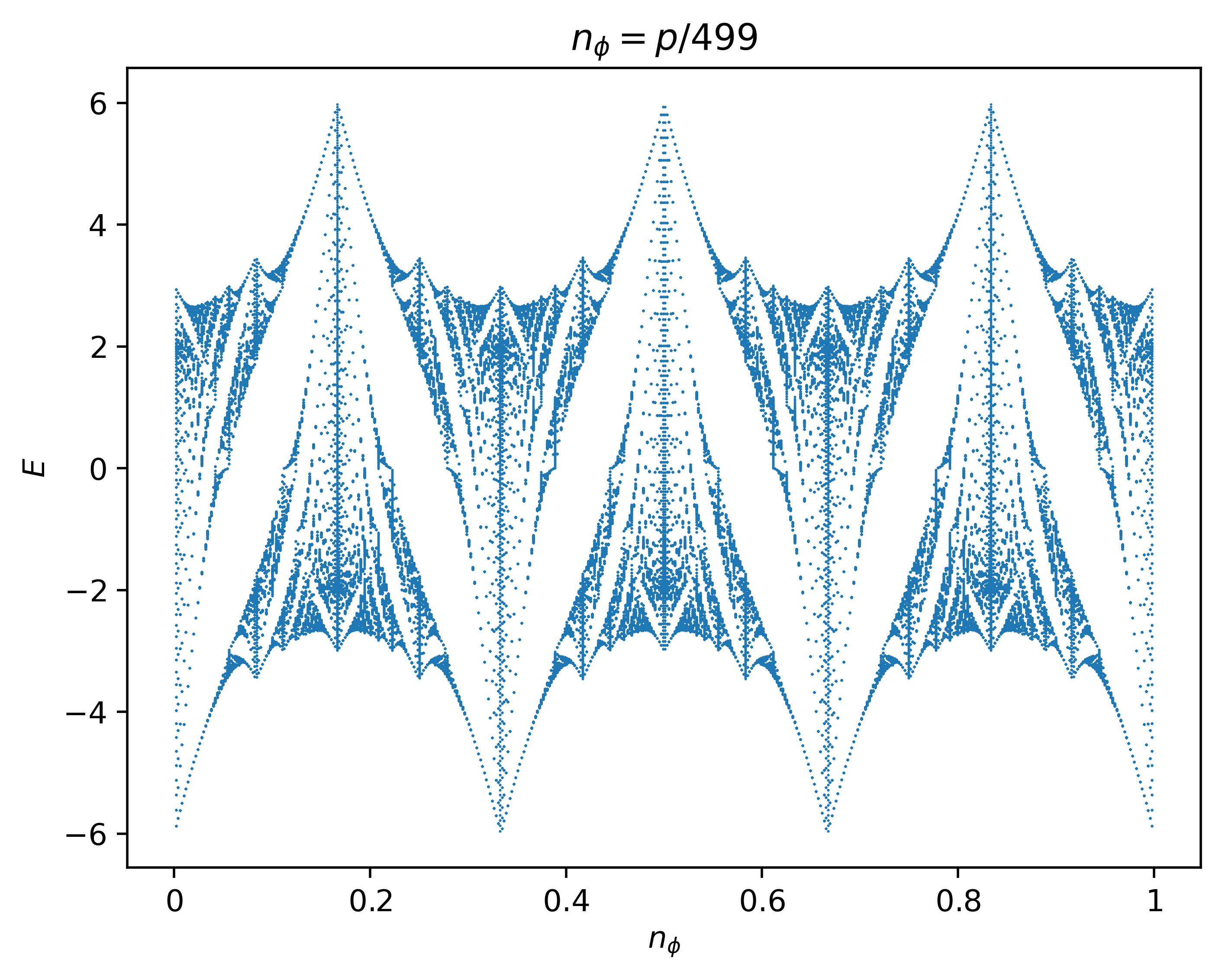
The Hofstadter model with 5th nearest-neighbor hopping on the honeycomb lattice. In this case, the model is equivalent to 2nd nearest-neighbor hoppings on a triangular sublattice. The ratio between the effective unit cell area spanned by the hopping terms and the minimal hopping plaquette area is 2, and so we append the flag --periodicity 2 to resolve the entire butterfly spectrum and fix any aperiodicity. The butterfly spectrum for 2nd nearest-neighbor hoppings on a triangular lattice is shown in Fig.4 of [Oh00].

butterfly -mod Hofstadter -q 499 -lat honeycomb -t 0 0 0 0 1 -period 2 -dpi 500 -save

_images/butterfly_honeycomb_q_499_t_0_0_0_0_1_alpha_1_theta_1_3_period_2_dpi_500.png

Kagome Lattice

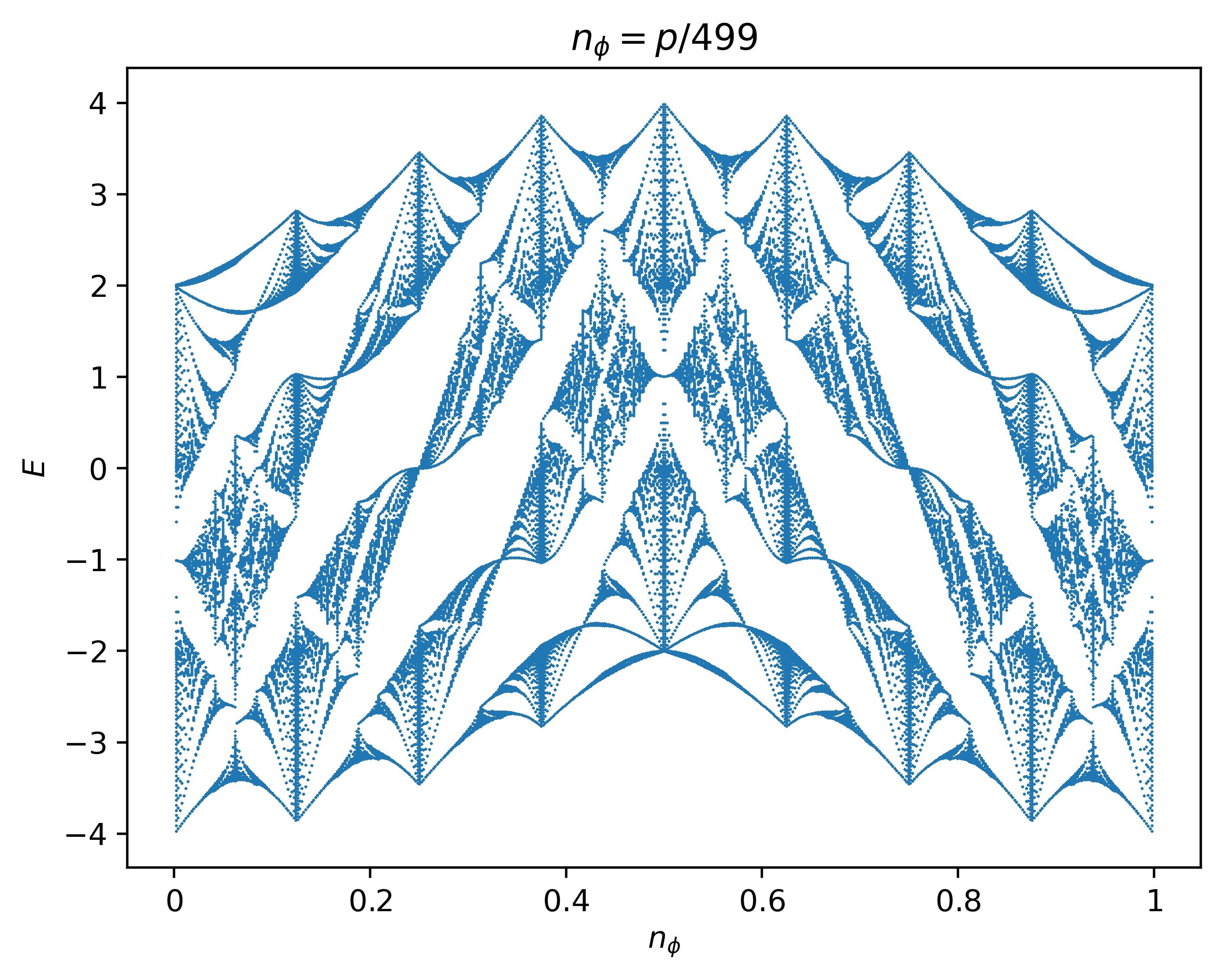
The Hofstadter model with nearest-neighbor hopping on the kagome lattice. In this case, the minimal plaquette area enclosed by particle hopping is 8 times smaller than the unit cell area, and so we append --periodicity 8 to resolve the entire butterfly spectrum and fix any aperiodicity. This butterfly is also plotted in Fig.3 of [Xiao03], Fig.3 of [Jing-Min09], and Fig.2(a) of [Du18].

butterfly -mod Hofstadter -q 499 -lat kagome -period 8 -dpi 500 -save

_images/butterfly_kagome_q_499_t_1_alpha_1_theta_1_3_period_8_dpi_500.png

Please contact Bart Andrews if you have any interesting contributions to the gallery!